Законы де моргана ударение

Видео:3.8 Де Морган правилаСкачать

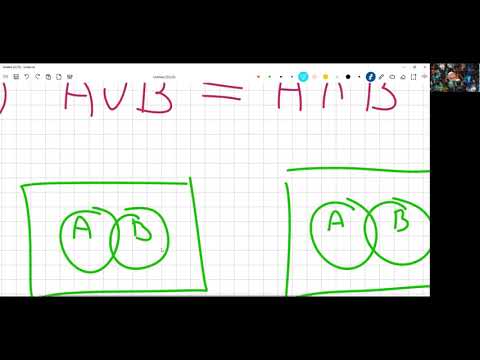
ЗАКОН ДЕ МОРГАНА

— общее название логических законов, связывающих с помощью отрицания конъюнкцию («и») и дизъюнкцию («или»). Названы именем англ. логика XIX в. А. де Моргана.

Один из этих законов можно выразить так: отрицание конъюнкции эквивалентно дизъюнкции отрицаний. Напр.: «Неверно, что завтра будет холодно и завтра будет дождливо, тогда и только тогда, когда завтра не будет холодно или завтра не будет дождливо».

Другой закон: отрицание дизъюнкции эквивалентно конъюнкции отрицаний. Напр.: «Неверно, что ученик знает арифметику или знает геометрию, тогда и только тогда, когда он не знает ни арифметики, ни геометрии».

В терминах символики логической (р, q — некоторые высказывания; & — конъюнкция; v — дизъюнкция;

— отрицание, «неверно, что»; = — эквивалентность, «если и только если») данные два закона представляются формулами:

q), неверно, что р и q, если и только если неверно р и неверно q;

q), неверно, что или р, или q, если и только если неверно р и неверно q.

На основе этих законов, используя отрицание, связку «и» можно определить через «или», и наоборот: «р и q» означает «Неверно, что не—р или не—q», «р или q» означает «Неверно, что не—р и не—q».

Напр., «Идет дождь и идет снег» означает «Неверно, что нет дождя или нет снега»; «Сегодня холодно или сыро» означает «Неверно, что сегодня не холодно и не сыро».

Видео:Законы де Моргана || Формулы де Моргана || Правило де МорганаСкачать

ЗАКОН ДЕ МОРГАНА

— отрицание, «невер­но, что»; = — эквивалентность, «если и только если») данные два закона представляются формулами:

q), неверно, что или р, или q, если и только если неверно р и неверно q. На основе этих законов, используя отрицание, связку «и» мож­но определить через «или», и наоборот: «р и q» означает «Невер­но, что не—р или не—q«, «р или q» означает «Неверно, что не—р и не—q«. Напр., «Идет дождь и идет снег» означает «Неверно, что нет дождя или нет снега»; «Сегодня холодно или сыро» означает «Не­верно, что сегодня не холодно и не сыро».

Смотреть больше слов в « Словаре по логике »

Смотреть что такое ЗАКОН ДЕ МОРГАНА в других словарях:

ЗАКОН ДЕ МОРГАНА

общее название логических законов, связывающих с помощью отрицания конъюнкцию («и») и дизъюнкцию («или»). Названы именем англ. логика XIX в. А. де Мор. смотреть

ЗАКОН ДЕ МОРГАНА

законы логики высказываний, связывающие отрицание с операциями конъюнкции и дизъюнкции, соответствующими логич. союзам «и» и неразделительному «или» естеств. языка. З. де М. в словесной формулировке были известны еще схоластич. логикам. В математич. логику введены англ. логиком де Морганом, однако не как законы логики высказываний, а как соответствующие законы логики классов. Имеют вид: (1) (A & B) экв. ( A) / ( B); (2) (A / B) экв. ( A) & ( B). Здесь знак «» означает операцию отрицания, знак «/» – дизъюнкцию (неразделительное «или»), а знак «&» – конъюнкцию высказываний (союз «и»). Закон (1) читается: отрицание конъюнкции высказываний А и В эквивалентно (равносильно) дизъюнкции отрицаний этих высказываний; закон (2) читается: отрицание дизъюнкции высказываний А и В эквивалентно конъюнкции их отрицаний. Лит.: Тарский . Введение в логику и методологию дедуктивных наук, пер. с англ., М., 1948, с. 88; Черч . Введение в математическую логику, [т.] 1, пер. с англ., М., 1960, с. 98, 394; De Morgan . Formal logic. L., 1926; Boehner P., Bemerkungen zur Geschichte der Morganschen Gesetze in der Scholastik, «Arch. Philos.», 1951, No 4, S. 113–46. Б. Бирюков. Москва. . смотреть

Видео:Законы де Моргана | 13/50 урок Информатики | ШколковоСкачать

Законы де моргана ударение

Законы де Моргана – это логические правила, установленные шотландским математиком Огастесом де Морганом, связывающие пары логических операций при помощи логического отрицания.

Огастес де Морган заметил, что в классической логике справедливы следующие соотношения:

not ( А and В ) = (not А ) or (not В )

not ( А or В ) = (not А ) and (not В )

В более привычной для нас форме данные соотношения можно записать в следующем виде:

Законы де Моргана можно сформулировать следующим образом:

I закон де Моргана: Отрицание дизъюнкции двух простых высказываний равносильно конъюнкции отрицаний этих высказываний.

II закон де Моргана: Отрицание конъюнкции двух простых высказываний равносильно дизъюнкции отрицаний этих высказываний.

Рассмотрим применение законов де Моргана на конкретных примерах.

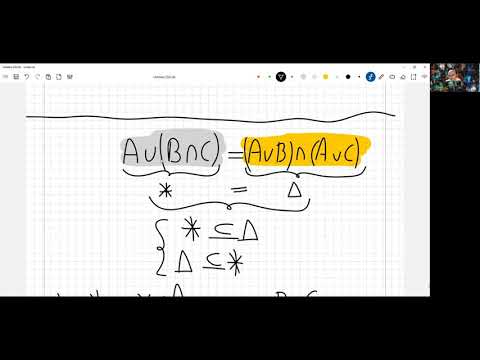
Пример 1. Преобразовать формулу так, чтобы не было отрицаний сложных высказываний.

Воспользуемся первым законом де Моргана, получим:

,

к отрицанию конъюнкции простых высказываний В и С применим второй закон де Моргана, получим:

,

.

В итоге мы получили равносильное высказывание, в котором нет отрицаний составных высказываний, а все отрицания относятся только к простым высказываниям.

Проверить справедливость решения можно с помощью таблиц истинности. Для этого составим таблицы истинности для исходного высказывания:

,

и для высказывания, полученного в результате преобразований, выполненных с помощью законов де Моргана:

.

🌟 Видео

Правила Де Моргана. Доказательство. Теория множеств.Скачать

Лекция 1. Определение множества. Законы де Моргана. Парадокс Рассела. Теорема ВейерштрассаСкачать

Законы де Моргана. ЛогикаСкачать

2.4 Разность множеств, законы де Моргана | Константин Правдин | ИТМОСкачать

Законы алгебры логики / Закон де Моргана + доказательство [Алгебра логики] #5Скачать

Свойства действий над множествамиСкачать

ЗАКОНЫ АЛГЕБРЫ ЛОГИКИСкачать

Лекция 67. Теорема де МорганаСкачать

Операции над множествамиСкачать

Множества и операции над нимиСкачать

Алгебра логики: Законы алгебры логики. Центр онлайн-обучения «Фоксфорд»Скачать

Закон Моргана за 50 минут | Биология ЕГЭ 10 класс | УмскулСкачать

Закон поглощения + доказательство. Преобразование логических выражений [Алгебра логики] #7Скачать

Введение в логику, урок 1: Базовые понятияСкачать

Закон МорганаСкачать

3.10 Пример - доказательство равенства двух множествСкачать

Томас Хант Морган и наследование мутаций у мушки дрозофилы (видео 8) | Классическая генетикаСкачать