Фреге ударение в фамилии (3 видео) | Русский язык. Правила написания

Содержание

Словари
Готлоб Фреге — об авторе
Информация
Биография
🎥 Видео

Видео:Как исчезают фамилии – сила случайных процессов // Vital MathСкачать

Словари

— Немецкий философ, сформулировавший идею «логицизма».

ФРЕГЕ (Frege) Готлоб (1848-1925) — немецкий логик, математик и философ, основоположник логицизма. Дал первую аксиоматику логики высказываний и предикатов, построил первую систему формализованной арифметики. Один из основоположников логической семантики.

Фре́ге Готлоб (Frege) (1848-1925), немецкий логик, математик и философ, основоположник логицизма. Дал первую аксиоматику логики высказываний и предикатов, построил первую систему формализованной арифметики. Один из основоположников логической семантики.

ФРЕГЕ Готлоб — ФРЕ́ГЕ (Frege) Готлоб (1848-1925), немецкий логик, математик и философ, основоположник логицизма. Дал первую аксиоматику логики высказываний и предикатов, построил первую систему формализованной арифметики. Один из основоположников логической семантики.

ФРЕГЕ Готлоб (Frege, Gottlob) (1848-1925), немецкий математик и философ. Родился 8 ноября 1848 в Висмаре. Получил математическое и естественнонаучное образование в Йенском и Геттингенском университетах, учился философии в Геттингене у Германа Лотце. В 1871 начал преподавать в Йене. В 1879, когда Фреге опубликовал 90-страничную работу Исчисление понятий (Begriffsschrift), с которой началась история современной логики, он получил должность экстраординарного профессора. Признание пришло к Фреге не сразу, а при жизни ограничивалось узким кругом наиболее выдающихся ученых. Логики Э.Шредер и Дж.Пеано, философ Э.Гуссерль знали об идеях Фреге, однако не сознавали в полной мере их значения. По-видимому, первым признал идеи немецкого мыслителя Б.Рассел в 1901. Р.Карнап и Л.Витгенштейн, к счастью для себя и последующих поколений, знали и ценили Фреге в юности. Карнап посещал лекции Фреге в 1910, 1913 и 1914, и именно Фреге в 1911 посоветовал Витгенштейну поехать учиться к Расселу. П.Журден изложил в деталях фрегевскую логику для англоязычных читателей в 1912, однако Фреге так и остался непризнанной фигурой, когда вышел в отставку в 1917. Умер Фреге в Бад-Кляйнене 26 июля 1925. Со времен Аристотеля и далее на всем протяжении Средних веков систематическая разработка формальной логики почти не выходила за пределы силлогистики. Готфрид Вильгельм фон Лейбниц придал новый импульс логическим исследованиям в 1666, применив аппарат алгебры. В этом алгебраическом духе прогресс спорадически возобновлялся, достигнув кульминационных точек в работах Дж.Буля, О.Моргана, Ч.С.Пирса и Э.Шредера в период 1847-1877. Однако только Фреге в 1879 отказался от алгебраических аналогий и разработал оригинальный символический и понятийный аппарат, пригодный для использования в универсальной и эффективной логической теории. По иронии судьбы, только отойдя от рабского подражания алгебре, Фреге выяснил истинную природу центрального понятия алгебры и логики — переменной. Обнаружилось родство между переменной и неопределенным местоимением. Математическая логика до сего дня сохраняет структуру, изложенную Фреге в Исчислении понятий, хотя с тех пор сам предмет пересек в своем развитии все мыслимые границы. В своей тонкой книжечке Фреге установил беспрецедентный стандарт формальной строгости: все шаги доказательства были описаны в терминах эксплицитно выраженных символических операций. Такой способ изложения привел в дальнейшем к революционным открытиям, касающимся масштаба и границ математического доказательства, в частности к работе К.Геделя (1931). Система Фреге выходила за пределы собственно логики и включала теорию множеств, а именно общую теорию классов, в том числе классов классов, классов классов классов и т. д. В своем труде Основания арифметики (Die Grundlagen der Arithmetik, 1884) и двухтомной работе Основные законы арифметики (Grundgesetze der Arithmetik, Bd. 1-2, 1893 и 1903) Фреге показал выводимость арифметики и других областей математики из логики и теории множеств, он также дал первую полную философскую интерпретацию понятия числа. В более поздних кратких статьях Фреге были затронуты вопросы семантики. Смысл, подчеркивал Фреге, следует отличать от значения. «Утренняя звезда» и «вечерняя звезда» обозначают одну и ту же планету, а именно Венеру, однако отличаются по смыслу. Когда выражения обозначают одно и то же, мы обычно можем заменить одно на другое в истинном высказывании, и это высказывание останется истинным. Однако в случае некоторых высказываний, особенно суждений о вере, такая подстановка оказывается невозможной. Например, мы хотели бы сказать, что Том верит в английское происхождение эйвонского барда, но не верит в английское происхождение автора Гамлета, хотя и то и другое обозначает одного и того же человека (Шекспира). Фреге утверждал, что в таких контекстах выражение перестает обозначать обычный объект и начинает обозначать то, что нормально является его смыслом. Эти и другие идеи Фреге имели большое значение для дальнейшего развития логической семантики.

Бирюков Б.В. Теория смысла Готлоба Фреге. — В кн.: Применение логики в науке и технике. М., 1960 Фреге Г. Предмет. Значение. Смысл. (Избранные работы.) М., 1996

(Frege, Gottlob) (1848-1925), нем. математик, логик и философ, профессор Йенского ун-та. Гл. труд Ф. Основной закон арифметики, т. 1-2 (1893-1903), посвящен логике высказываний и предикатов. Ф. дал первую ее аксиоматику, а также построил первую систему формализованной арифметики. Его строгая систематизация логики легла в основу послед, развития мат. логики, а филос. анализ значения — логической семантики и лингвистики (языкознание). Идеи Ф. внимательно изучались Расселом и Витгеншгейном, а затем стало достоянием большинства филос. направлений Англии и США 20 в.

Видео:#СКЛОНЕНИЕ ФАМИЛИЙ // Как склоняются русские, заимствованные, женские, мужские... все-все фамилииСкачать

Готлоб Фреге — об авторе

Видео:Треугольник Фреге | Дефляционная теория истиныСкачать

Информация

Видео:Семинар «НПММвЯ» памяти А. А. ЗализнякаСкачать

Биография

Фридрих Людвиг Готлоб Фреге — немецкий логик, математик и философ. Представитель школы аналитической философии.

Сформулировал идею логицизма, то есть направление в основаниях математики и философии математики, основным тезисом которого является утверждение о «сводимости математики к логике».

Отец Фреге был школьным учителем, преподававшим математику. Фреге начал свое высшее образование в Йенском университете в 1869 г. Через два года он переехал в Гёттинген, где он и защитил в 1873 г. свою диссертацию по математике «Über eine geometrische Darstellung der imaginären Gebilde in der Ebene» (О геометрическом представлении воображаемых объектов на плоскости). После защиты диссертации он вернулся в Йену, где под руководством Аббе написал хабилитационную работу «Rechnungsmethoden, die sich auf eine Erweitung des Größenbegriffes gründen» (Методы расчётов, которые основаны на расширении понятия размерности) (1874) и получил место приват-доцента (1875). В 1879 г. он стал экстраординарным, в 1896 г. — ординарным профессором. Из его непосредственных учеников широко известен только Рудольф Карнап (впоследствии — один из членов Венского кружка и автор ряда важных работ по философии науки). Поскольку все дети Фреге умерли до достижения зрелости, в 1905 г. он взял в дом приёмного сына.

Популяризация его идей Карнапом, Бертраном Расселом и Людвигом Витгенштейном сделала Фреге известным в определенных кругах ещё в 1930-е гг. В англоязычном мире его работы стали широко известны только после Второй мировой войны, в значительной степени благодаря тому, что многие логики и философы, считавшие наследие Фреге важным вкладом в развитие философской мысли (например, Рудольф Карнап, Курт Гёдель и Альфред Тарский), вынуждены были эмигрировать в США. Они способствовали появлению английских переводов основных работ Фреге, которые и принесли ему широкую известность.

Видео:ЕГЭ 2017. Литература. Двусложные размеры (ямб и хорей)Скачать

Фридрих Людвиг Готлоб Фреге (Friedrich Ludwig Gottlob Frege) — немецкий логик, математик и философ.

Родился 8 ноября 1848 в Висмаре. Образование получил в университетах Йены, а затем Гёттингена, где в 1873 защитил под руководством Эрнста Шеринга диссертацию на ученую степень доктора философии. Вернулся в Йену, где в 1874 защитил габилитационную диссертацию (на право преподавания в университетах), и в том же году был назначен приват-доцентом Йенского университета. В 1879 получил должность профессора математики. В общей сложности Фреге преподавал в Йенском университете в течение 44 лет, прочитал курсы лекций по различным математическим дисциплинам – аналитической геометрии, алгебраическому анализу, высшей алгебре, теории функций, теории чисел и др. Лекции по логико-математической тематике читал с 1883 . Академической карьерой Фреге был во многом обязан своему учителю и другу Эрнсту Аббе.

Придерживался консервативных, антидемократических и националистических взглядов. Занимал маргинальное положение в научном сообществе Германии; занимался изысканиями в области философии и в области логических оснований математики, что в то время не считалось престижным. Вступил в полемику с признанными научными авторитетами, что вызывало раздражение коллег.

В 1879 Фреге опубликовал 90-страничную работу Исчисление понятий (Begriffsschrift), которая из-за новизны концепции и громоздкой символики была принято сдержанно. В 1884 опубликовал Основания арифметики (Die Grundlagen der Arithmetik), в 1893 выпустил первый том Основных законов арифметики (Grundgesetre der Arithmetik; второй том – 1903 ). В тот же период Фреге создал ряд трудов по логической семантике и анализу языка: Смысл и денотат ( 1892 ), Понятие и вещь ( 1892 ), Функция и понятие ( 1891 ), ныне признанных классическими.

В 1902 , передав в печать второй том «оснований арифметики», Фреге получил письмо от Бертрана Рассела, где сообщалось о формальном противоречии в предложенном Фреге обосновании арифметики (парадокс Рассела), разрешить которое Фреге тщетно пытался до конца своей жизни. Однако именно Рассел принес Фреге широкую известность, ибо в изложении Рассела (специальное приложение к Основаниям математики, 1903) концепция Фреге стала доступной широкому кругу читателей. В предисловии к первому тому Оснований математики А.Н.Уайтхед и Рассел дают высокую оценку его логико-математической концепции. П.Журден подробно изложил фрегевские идеи и опубликовал их в серии статей, посвященных развитию логики и оснований математики. Эти обстоятельства способствовали признанию вклада Фреге в науку.

Фреге оказал большое влияние на Р.Карнапа и Л.Витгенштейна, которые в период с 1910 по 1914 слушали его лекции об Исчислении понятий. Именно Фреге в 1911 посоветовал Витгенштейну поехать учиться к Расселу.

Умер Фреге в Бад-Кляйнене 26 июля 1925 .

Фреге впервые осуществил дедуктивно-аксиоматическое построение логики высказываний и логики предикатов. Впоследствии метод построения теории путем формальной дедукции был распространен им на арифметику. В рамках аксиоматического исчисления он предъявлял к доказательствам гораздо более высокие требования, чем это было принято ранее: «При переходе к новому утверждению ни одна из предпосылок не должна остаться незамеченной, каждая аксиома должна быть установлена». В своих работах Фреге исследовал такие фундаментальные понятия, как «функция», «переменная», «понятие», «смысл», «истинностное значение» и др. Ввел множество различений, которые оказались важными для последующего развития логики, такие, как различие между формулировкой высказывания и утверждением, что это высказывание истинно, между отношением принадлежности и отношением включения, между объектом х и множеством 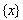, включающим один этот объект и др.

Фреге является основателем современной логической семантики. В работе Смысл и денотат (известной также под названием О смысле и значении) изложена теория имени, включающая номинативную теорию предложения. Именно эта теория легла в основу того, что впоследствии было названо «семантическим треугольником» (или «треугольником Фреге»). Фреге исходил из того, что два разных знака могут указывать на один и тот же предмет: так два выражения Утренняя звезда и Вечерняя звезда указывают на один и тот же предмет (одну и ту же вещь) – планету Венеру, но имеют разный смысл. Таким образом, знак (будь то слово, словосочетание или графический символ) может мыслиться не только в связи с обозначаемым, т.е. с тем, что можно было бы назвать денотатом знака, с вещью, которую этот знак обозначает, но и с тем, что Фреге называл смыслом знака, призванным отображать способ представления обозначаемого данным знаком. Так ‘Утренняя звезда’ и ‘Вечерняя звезда’ – это два разных способа представления для планеты Венеры. Выражения, обозначающие вещь в широком смысле слова (но не понятия или отношения), Фреге называл именами собственными, выражающими некоторый смысл и обозначающими (называющими) некоторый денотат. Что касается повествовательных предложений, то у них также есть смысл – суждение (мысль), которую они выражают, и денотат – одно из двух истинностных значений (Истина или Ложь), приравниваемые в концепции Фреге к абстрактным вещам. Если заменить в повествовательном предложении одно имя собственное на другое с тем же денотатом, но другим смыслом, то смысл предложения изменится, но его денотат, т.е. его истинностное значение, останется прежним. Так предложения Утренняя звезда – это небесное тело, освещаемое солнцем и Вечерняя звезда – это небесное тело, освещаемое солнцем выражают разные суждения (имеют различный смысл), но один и тот же денотат, одно и то же истинностное значение. Таким образом, все истинные предложения в концепции Фреге имеют одинаковый денотат, так же как и все ложные, в то время как имена собственные называют бесконечное множество различных вещей. Суждение (смысл предложения) отличается от утверждения тем, что в утверждении сделан шаг от мысли к денотату, а именно к истинностному значению высказывания: «Слово утверждение я понимаю не просто как понимание некоторого суждения, но как признание его истинности, т.е. как его принятие».

Понятия и отношения также имеют имена (слова, выражения или графические символы), которым соответствует определенный смысл и денотат – а именно, обозначаемое ими понятие или отношение. Денотат имени понятия отличается от денотата имени собственного или повествовательного предложения тем, что он вещью не является, а также тем, что он ненасыщен. «Все части предложения, – писал Фреге, – не могут быть замкнуты, должна найтись хотя бы одна в каком-то смысле ненасыщенная, или предикативная часть – в противном случае соединение частей в единое целое оказывается невозможным». Вещи могут подпадать или не подпадать под понятия: так, предложение Утренняя звезда (есть) планета, где Утренняя звезда является именем собственным, а планета именем понятия, указывает на то, что объект Утренняя звезда подпадает под понятие планета, а грамматический предикат обозначает это понятие. Понятие является частным случаем функции, которая также обладает свойством ненасыщенности (Функция и понятие).

а также многие другие факторы, например, тот факт, что выражение понятие «лошадь» является именем собственным, т.е. его денотатом является некоторая абстрактная вещь, а не понятие – «в то время как город Берлин остается городом, а вулкан Везувий – вулканом». Здесь, как и во многих других случаях, Фреге применяет характерный принцип абстракции, вводит в рассмотрение абстрактные предметы, приравниваемые им к объектам реального мира (тот же самый «прием» он использует, в частности, определяя истинностные значения Истина и Ложь как абстрактные вещи).

Тем не менее Фреге не пытался развить сколько-нибудь общую лингвистическую теорию. Многие схемы, предложенные Фреге для описания «вводящих в заблуждение» особенностей естественного языка, носят незавершенный характер, Так, например, нигде нет указания на то, что же является смыслом выражений в косвенном употреблении, если таковой вообще существует.