Ферма ученый математик ударение

Видео:Математика это не ИсламСкачать

Пьер Ферма: биография, фото, открытия в математике

Пьер де Ферма – один из самых великих ученых в истории Франции. К его достижениям можно отнести создание таких трудов, как теория вероятностей и чисел, он является автором выдающихся теорем и первооткрывателем ряда математических свойств. С самых юных лет его родители уделяли огромное внимание образованию сына и, скорее всего, именно это повлияло на становление грандиозного ума. Всегда спокойный и деятельный, любознательный и строгий, ищущий и находящий – все это Пьер Ферма. Краткая биография поможет читателю подчерпнуть для себя все самое интересное об этой колоссальной по величине личности математика.

Видео:Математик и чертСкачать

Ранние этапы

Пьер был рожден во Франции. Он является одним из первооткрывателей и создателей теории чисел, а также аналитической геометрии.

Длительное время говорили, что Пьер Ферма был рожден в 1595 году в Тулузе, но к середине девятнадцатого века в городе Бомоне в архивах была обнаружена запись, в которой было сказано, что летом 1601 года у советника города Доминика Ферма и его супруги появился на свет сын Пьер. Известно, что Доминик Ферма был очень уважаемым человеком в городе. Он был торговцем кожей. Детские годы Пьер провел рядом с родителями, а когда пришло время получать образование, он уехал в Тулузу – самый ближний город с университетами. Хорошенько изученное право на скамье университета дало Пьеру возможность работать адвокатом, но юноша решил перейти на службу к государству. В 1631 году Пьер был зачислен на место советника касс в парламент Тулузы. В это время Ферма уже был в браке с дочерью советника парламента, в котором он работал. Его жизнь была очень тихой и спокойной. Но благодаря ему сегодня люди, изучающие математику, могут почерпнуть для себя много интереснейшей информации, которая поистине бесценна. Даже в школьной программе активно уделяется внимание теме «Пьер Ферма и его открытия».

Видео:Математик и чёрт (звуковая дорожка исправлена) 1972 год.Скачать

Увлечение историей

В юности будущий математик славился как тончайший знаток истории (в особенности античности), за его помощью обращались при издании классики Греции. Он оставил комментарии к трудам Синезуга, Атенея, Полюнуса, Фронтина, Теона Смирнского, внес правки в тексты Секста Эмпирика. Многие считают, что он с легкостью мог бы оставить свой след как выдающийся греческий филолог.

Однако благодаря тому, что он избрал иной путь, свет увидели его грандиозные по своей величине исследования. И поэтому большинство людей знает, что Пьер Ферма – математик.

О работах его при жизни в основном становилось известно посредствам широкой переписки, которую Ферма вел с иными учеными. Сборник сочинений, который он не единожды пробовал составить, так и не был претворен в жизнь. Собственно говоря, это логичный итог при такой загруженности на основной работе в суде. При жизни Пьера ни одно из массы его сочинений не было опубликовано.

Видео:ВЕЛИКАЯ ТЕОРЕМА ФЕРМА 😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

Пьер Ферма: открытия в математике

Одна из первых работ в области математики у Пьера Ферма — возобновление двух утраченных книг-сочинений Аполлония под названием «О плоских местах». Колоссальную заслугу Пьера перед наукой большинство видит во введении им в аналитическую геометрию бесконечно малых величин. Он сделал этот крайне важный шаг в 1629 году. Также в конце двадцатых годов Пьер Ферма нашел способы нахождения касательных и экстремумов. А уже в 1636-м полностью завершенное описание метода нахождения было передано в руки Мерсенну, и с данным трудом мог ознакомиться кто угодно.

Видео:Визуализация теоремы ФермаСкачать

Полемика с Декартом

В 1637-38 годы французский математик Пьер Ферма бурным образом полемизировал с не менее выдающимся математиком Рене Декартом. Полемика возникала вокруг «Метода нахождения минимумов и максимумов». Декарт не до конца разобрался в методе и не понял его, по этой причине он подверг его несправедливой критике. Летом 1638 года Пьер Ферма посылает Мерсенну для передачи Декарту обновленное и более насыщенное подробностями изложение своего метода. В его письме отражается его сдержанный характер, потому что оно написано в крайне сухой и спокойной манере, но в то же время в нём есть некоторая доля иронии. В его письме содержится даже прямая насмешка над недопониманием Декарта. Ферма ни разу не вошел в бессмысленную и несдержанную полемику, он постоянно придерживался ровного и холодного тона. Это был не спор, а, скорее, беседа походила на общение преподавателя со студентом, который что-то не понял.

Видео:Деконструкция – Математик и чёрт (рассказывает Алексей Савватеев)Скачать

Систематика вычисления площадей

До Пьера Ферма способы нахождения площадей были разработаны итальянцем Кавальери. Однако к 1642 году Ферма открыл способ нахождения площадей, которые ограничены любыми «параболами» и «гиперболами». Ему удалось доказать, что площадь практически любой неограниченной фигуры все-таки может иметь конечное значение.

Видео:Математик и черт, 1972Скачать

Задача спрямления кривых

Одним из самых первых начал изучение задачи на вычисление длин дуг кривых. Ему удалось подвести решение задачи к нахождению некоторых площадей. К вычислению площади сводились все задачи на кривые. Оставалась одна капля для того, чтобы ввести новое и более абстрактное понятие «интеграл».

В дальнейшем весь положительный исход способов по определению «площадей» был в поиске взаимосвязи с «методом экстремумов и касательных». Есть сведения, что Ферма уже видел четкую взаимосвязь, но ни один из его трудов не отражает этой точки зрения.

В отличие от большинства своих сотоварищей по делу, Пьер де Ферма являлся чистейшим математиком и никогда не пытался исследовать другие отрасли науки. Вероятно, именно по этой причине его мощнейший вклад во всю математику настолько глубок и велик.

Видео:Великая теорема ФермаСкачать

О теории чисел

Самым главным вкладом Ферма в математику и по сей день считают создание абсолютно новой дисциплины – числовой теории. Ученый на протяжении всей своей трудовой деятельности интересовался арифметическими задачами, которые он порой придумывал и загадывал сам. В процессе нахождения ответов на вопросы, поставленные в задачах, Ферма частенько открывал что-то полностью новое и уникальное. Новые алгоритмы и законы, теоремы и свойства — все это когда-то легло в основу теории чисел, сегодня известной каждому школьнику.

Видео:Малая теорема Ферма и теорема Эйлера | Ботай со мной #037 | Борис Трушин !Скачать

Вклад в труды иных ученых

Таким образом, Пьер Ферма обнаружил закономерности для натуральных чисел и установил их на века. Труды о натуральных числах называются «теоремы арифметики». Одной из них, например, является знаменитая «малая теорема». В дальнейшем она послужила Эйлеру как частный случай для его трудов. Также известно, что именно работы Пьера Ферма задали основу теореме Лагранжа о сумме 4 квадратов.

Видео:Лжецы Ферма [Numberphile]Скачать

Теорема Ферма

Конечно же, больше всего из трудов Пьера выделяется его великая и могучая теорема. Она многие годы и даже десятилетия заставляла «ломать головы» величайших математиков, и даже после того как она была опубликована в 1995 году, новые и очень разнообразные методы ее доказательств все еще поступают на кафедры с математическим уклоном во многие университеты мира.

Хотя Ферма оставил только краткие изложения своих трудов и обрывочную информацию, именно его открытия дали толчок многим другим выдающимся гениям математики. В его честь назвали один из наиболее престижных и старых лицеев во Франции – Лицей имени Пьера Ферма в Тулузе.

Видео:"Жизнь после великой теоремы Ферма: АВС-гипотеза"Скачать

Смерть ученого

Во время своей активнейшей деятельности в области математики Ферма довольно быстрыми темпами продвигается вверх в судебном деле. В 1648 году Пьер становится членом Палаты эдиктов. Настолько высокая должность свидетельствовала о высочайшем положении ученого.

В Кастре, где Ферма стал эдиктом, он умирает при выезде на очередную сессию суда. Смерть пришла к математику в возрасте всего 64 лет. Старший сын ученого взялся донести труды отца людям и выпустил ряд его исследований.

Таков был Пьер Ферма. Биография его была насыщенной, а жизнь оставила след на все времена.

Труды этого гиганта математики невозможно переоценить и недооценить, ведь они заложили прочный фундамент для многих исследователей. Пьер Ферма, фото (портреты) которого приведены в статье, имел твердый характер, который всю жизнь помогал ему добиваться своих целей.

Видео:Высшая математика. Теорема Ферма, Ролля, Лагранжа, КошиСкачать

Словари

1. Частное хозяйство или сельскохозяйственное предприятие на собственном или арендованном участке земли.

2. Специализированное животноводческое или звероводческое хозяйство.

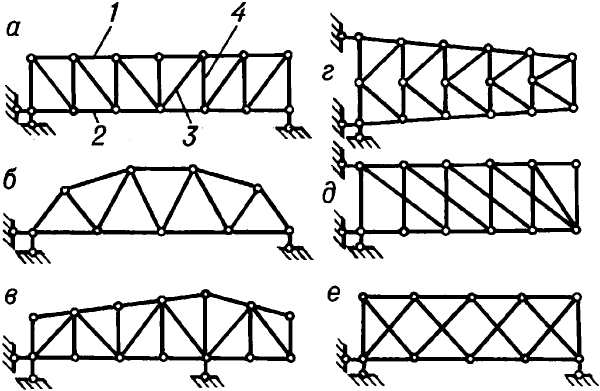
Инженерное сооружение в виде несущей конструкции покрытия здания, пролётного сооружения моста или гидротехнического сооружения, состоящее из соединённых между собою балок, стержней, изготовленных из железобетона, стали и т.п.

ФЕ́РМА — сущ., ж., употр. сравн. часто

Морфология: (нет) чего? фе́рмы, чему? фе́рме, (вижу) что? фе́рму, чем? фе́рмой, о чём? о фе́рме; мн. что? фе́рмы, (нет) чего? фе́рм, чему? фе́рмам, (вижу) что? фе́рмы, чем? фе́рмами, о чём? о фе́рмах

1. Ферма — это вид частного владения, обычно земельный участок, который состоит из полей и строений и на котором выращивают зерновые культуры или разводят животных.

Коневодческая, овцеводческая, кролиководческая ферма. | Молочная ферма. | Песцовая ферма. | Хозяин фермы. | Владеть фермой.

2. Рыбная ферма — это участок реки или моря, где разводят промысловую рыбу.

Мидийная, устричная ферма.

3. В архитектуре фермой называется несущая конструкция здания, пролётного сооружения моста, гидротехнического сооружения и т. п., которая состоит из соединённых между собой металлических стержней.

Стальная ферма. | Мостовая, решётчатая ферма. | Ферма перекрытия. | Арочная, балочная, стропильная ферма. | Монтаж, установка фермы.

ФЕ́РМА 1 , фермы, жен. (франц. ferme) (с.-х.).

1. Хозяйственное предприятие, занимающееся какой-нибудь специальной отраслью сельского хозяйства. Животноводческая ферма. Молочная ферма.

2. В капиталистических государствах — частное сельскохозяйственное предприятие на собственном или арендуемом участке, хутор.

ФЕ́РМА 2 , фермы, жен. (франц. ferme) (тех.). Сооружение, представляющее собой конструкцию из стержней, брусьев. Стальная ферма. Арочная ферма. Балочная ферма. Стропильная ферма. Мостовые фермы.

1. Животноводческое подразделение в хозяйстве совхоза или колхоза, а также специализированное звероводческое хозяйство. Молочная ф. Племенная ф. Песцовая ф.

2. Частное хозяйство или сельскохозяйственное предприятие на собственном или арендуемом земельном участке.

II. ФЕ́РМА, -ы, жен. Сооружение из скреплённых стержней, брусьев. Стальная ф. Мостовая ф.

| прил. фермовый, -ая, -ое и ферменный, -ая, -ое (спец.).

ФЕРМА — жен., франц. заимка сиб. хутор южн. мыза петерб. особенно для скота. Фермер, хозяин или съемщик, кортомщик хутора.

Предприятие, находящееся в частной собственности, расположенное на собственной или арендуемой земле.

Кажется, я все делаю, чтобы не отстать от века: крестьян устроил, ферму завел, так что даже меня во всей губернии красным величают; читаю, учусь, вообще стараюсь стать в уровень с современными требованиями, — а они говорят, что песенка моя спета (Т.).

Предприятие (чаще всего животноводческое) в составе колхоза или совхоза.

Летом он [Алеша] пас колхозных коров, зимой был скотником… на ферме… (Шукш.).

Часть сооружения (покрытия здания, пролетного сооружения моста, гидротехнического сооружения и т. п.), представляющая собой несущую конструкцию, состоящую из скрепленных между собой стержней, брусьев.

Центральная ферма моста обрушилась.

1. ФЕ́РМА, -ы; ж. [франц. ferme]

1. Отдельное специализированное, обычно животноводческое хозяйство. Коневодческая ф. Молочная ф. Животноводческая ф. Песцовая ф. Племенная ф. Работать на ферме дояркой.

2. Частное хозяйство на собственном или арендуемом земельном участке. Организовать ферму. Владеть фермой.

2. ФЕ́РМА, -ы; ж. [франц. ferme] Архит. Несущая конструкция покрытия здания, пролётного сооружения моста, гидротехнических сооружений и т.п., состоящая из соединённых между собой стержней. Стальная ф. Мостовая ф. Арочная, балочная, стропильная ф. Ф. плотины, подъёмного крана.

◁ Фе́рменный, -ая, -ое. Ф. пролёт. Ф-ая стойка.

фе́рма (франц. ferme, от лат. firmus — прочный) (в строительной механике), геометрически неизменяемая стержневая система, у которой все узлы принимаются при расчёте шарнирными. Металлические, железобетонные, деревянные и комбинированные фермы применяют в покрытиях зданий, мостах и др.

ФЕРМА (франц. ferme — от лат. firmus — прочный), в строительной механике — геометрически неизменяемая стержневая система, у которой все узлы принимаются при расчете шарнирными. Металлические, железобетонные, деревянные и комбинированные фермы применяют в покрытиях зданий, мостах и др.

1. Отдельное специализированное, обычно животноводческое хозяйство совхоза, колхоза или учебного сельскохозяйственного заведения.

Коневодческая ферма. Молочная ферма.

На другой день мы осматривали лисью ферму, где в клетках содержится много серебристо-черных лисиц. Туров, Очерки охотника натуралиста.

2. В капиталистических странах: частное хозяйство на собственном или арендуемом земельном участке.

Ферма [в Исландии] возникала там, где находился участок земли с мало-мальски годным почвенным слоем. Первенцев, В Исландии.

Несущая конструкция покрытия здания, пролетного сооружения моста, гидротехнических сооружений и т. д., состоящая из соединенных между собой стержней.

Огромный металлический мост с высокими овальными фермами еще издали привлек внимание Малова. Уксусов, После войны.

Ферма́, нескл., муж.: при́нцип Ферма́, теоре́ма Ферма́

фе́рма. Произношение [фэ́рма] устарело.

фе́рма, фе́рмы, фе́рм, фе́рме, фе́рмам, фе́рму, фе́рмой, фе́рмою, фе́рмами, фе́рмах

сущ., кол-во синонимов: 24

ранчо, усадьба, хутор; умет, племхоз, фольварк, хозяйство, консоль

Syn: ранчо, усадьба, хутор

частное сельскохозяйственное предприятие на собственном или арендуемом участке

У нас скотоводческая ферма в Баварии, и выгоднее кормить несколько лишних голов скота, чем лишних рабочих.

специализированное животноводческое подразделение сельскохозяйственного предприятия

Наконец, под Детским Селом построена молочная ферма ЛСПО на 1200 голов скота.

Для каждого узла фермы серверов можно отдельно выполнять резервное копирование и восстановление, а также устанавливать квоты для дискового пространства, занимаемого узлом и автоматически отправлять владельцу узла уведомления при достижении предельного размера узла.

Во время параллельной миграции определяются и конфигурируются новые фермы серверов приложений параллельно существующему окружению. В определённый момент времени они заменяют старые фермы и работают параллельно с другими фермами, не имея с ними общих точек соприкосновения.

сооружение из скреплённых концами стержней, брусьев и т. п.

Ферма весом не менее четырёхсот тонн была поднята нами за три месяца на высоту двенадцати метров над водой очень простыми приёмами.

Здесь, между кирпичными быками, торчит рухнувшая в реку ферма взорванного моста.

1. фе́рм/а¹ (молочная).

2. фе́рм/а² (несущая конструкция здания, моста и т. п.).

Заимств. в первой половине XIX в. из франц. яз., где ferme — производное от fermer «запирать». Ферма буквально — «закрытый двор».

народн. хе́рма (Мельников). Из франц. ferme — то же: fermer «запирать» (Гамильшег, ЕW 413).

ФЕРМА I ы, ж. ferme f.

1. Здание хозяйственного назначения в поместье, усадьбе и т. п. БАС-1. Лиза вышла из лесу, перебралась через поле в сад и опрометью побежала в ферму, где Настя ожидала ее. Пушк. Барышня-крестьянка. Аркадий сделался рьяным хозяином, и «ферма» уже приносит значительный доход. Тург. Отцы и дети. Здравствует ли на ферме Твоя корова, которую Ты выбрала себе еще теленком. 18. 5. 1883. К. К. Романов — А. Кузнецовой-Князевой. // ДН 2000 11 129. || Сельскохозяйственное предприятие в капиталистических странах, основанное на собственной или арендованной земле. БАС-1. Разсуждали .. как бы здесь в деревнях завести фермы. 1765. Порошин Зап. // РС 1881 31 315. [Князь :] Да в ферме не забудь ты графу показать Мои плантации. 1819. Шаховской Пустодомы. // Стих. ком. 2 255. Хозяйство. В воспоминаниях моих сохранился образец такой русской фермы. М. Фонвизин 2 102. В Лифляндии и Курляндии нет деревень, подобных русским. Там фермы, рассеянные около замков. Герц. О разв. революц. идей в России. Для нас теперь существенные вопросы — вольнонаемный труд, наиболее интересное устройство ферм, кондиции с рабочими, учет рабочих или уроки их. 1. 9.1860. Н. Анненков. // Славяне 23. [Никанор (слуга):] Как не слыхать.. Сегодня сам обед заказывал, как встал, послал меня на ферму к старичку Чарову за букетаи. Будувар убрали в лучшем вкусе. Н. Вучетич На крутых берегах. // Слово 1879 1 1 91. Из сада поехали на ферму Шелестовых. Здесь .. вызвали жену приказчика Прасковью и потребовали парного молока. Чехов Учитель словесности.

2. Хозяйство при сельскохозяйственном учебном заведении, имеющее образовательное значение. БАС-1. Присужденных за проступки <государственных крестьян> отсылать преимущественно на образцовыя фермы и хутора. 1839. ПСЗ-2 14 (1 298). В тех округах, где имеются фермы, врачебный надзор над ними поручается окружным Врачам. 1851. ПСЗ-2 26 (2 184). Недалеко от Липецка есть лесная ферма, где учится мой брат. 26. 6. 1869. Г. Успенский — И. А. Долганову. // У. 9-9 207. Простые бородатые казаки называют образцовую ферму не фермой, а «сирмой». Л. Сладков Семейн. хроника. // Юность 1999 5 89. ♦ Fermes-écoles. Школы при частных экономиях будут, подобно французским fermes-écoles, больше служить дешевой эксплуатации и работе учеников, чем интересам их обучения. РМ 1885 8 1 154.

3. устар. Название молочного магазина. Молочные фермы. На вывеске <магазина> рисуют женщину в сарафане и кокошнике, которая доит корову. 1892. Светлов 1998 31.

4. Хозяйственное предприятие совхоза или колхоза, занимающееся той или иной специальной отраслью сельского хозяйства. Колхозная ферма. Животноводческая ферма. БАС-1. — Лекс. САН 1847: фе/рма.

ФЕРМА II ы, ж. ferme f. Инженерное сооружение, состоящее из соединенных между собой стержней. Стропильная ферма. БАС-1. Сооружение из скрепленных стержней. брусьев. Ож. 1986. Особенно трудно было перебраться через разрушенный мост. Ферма провалилась вниз серединой. 8. 10. 1914. Вел. кн. А. В. Романов Дн. // Октябрь 1998 4 143. Особенностью современных американских деревянных ферм являются специальные металлические болты и соединители (коннекторы), которыми крепятся соединения. НИЖ 1944 1-2 31. Фасонка металлическая пластинка той или иной формы, конструктивно соединяющая несущие элементы металлической конструкции (например стержни в узлах фермы). Лессельрот. Полуферма. РРП 1953. — Лекс. Толль Прил. 1866: фермы; Михельсон 1866: ферма; Даль-3: фе/рма.

ФЕРМА III ы, ж. ferme f. «Ферму» или откупную систему распространили <во Франции Людовика XIV > даже на почту и подати. 1900. Трачевский 413.

ФЕРМА (фр. ferme, от лат. firme — крепко, прочно). 1) арендуемый деревенский дом, при котором есть сад, скотный двор, а иногда и пахотная земля; то же, что мыза, хутор. 2) в Петербурге молочная ферма есть просто приют для дойных коров, откуда отпускают молоко.

— Хозяйство, вытесняющее колхозы.

— Великую теорему этого математика не могли доказать в течение 350 лет, а доказал лишь в 1995 году Эндрю Уайлс.

— Место работы доярки.

— Сельскохозяйственное предприятие, хутор.

— Фильм Джорджа Роя Хилла «Забавная . ».

— Сооружение из скреплённых стержней, брусьев.

— Роман американского писателя Джона Апдайка.

ФЕРМА (Fermat) Пьер (1601-65) — французский математик, один из создателей аналитической геометрии и теории чисел (теоремы Ферма). Труды по теории вероятностей, исчислению бесконечно малых и оптике (принцип Ферма).

ФЕРМА (в строительстве) — ФЕ́РМА (франц. ferme, от лат. firmus — прочный), в строительной механике — геометрически неизменяемая стержневая система, у которой все узлы принимаются при расчете шарнирными. Металлические, железобетонные, деревянные и комбинированные фермы применяют в покрытиях зданий, мостах и др.

ФЕРМА, индивидуальное сельскохозяйственное предприятие, ведущееся на собственной или арендованной земле с целью получения товарной сельскохозяйственной продукции и денежного дохода; связано, как правило, с поселением хуторского типа. В современных условиях в развитых странах многие фермерские хозяйства втягиваются в систему межотраслевых связей, организуемых промышленными предприятиями и кооперативами на основе вертикальной интеграции, становясь при этом частями крупных агропромышленных объединений.

ФЕРМА (от латинского firmus — прочный) (строительное), стержневая несущая конструкция, у которой соединения стержней в узлах при расчете принимаются шарнирными. Металлические, железобетонные, деревянные и комбинированные фермы применяют в покрытиях зданий, пролетных строениях мостов, гидротехнических сооружениях и др.

Видео:#232. Малая теорема Ферма и псевдопростые числаСкачать

Пьер Ферма

В одном из некрологов Пьеру Ферма говорилось: «Это был один из наиболее замечательных умов нашего века, такой универсальный гений и такой разносторонний, что если бы все ученые не воздали должное его необыкновенным заслугам, то трудно было бы поверить всем вещам, которые нужно о нем сказать, чтобы ничего не упустить в нашем похвальном слове».

К сожалению, о жизни великого ученого известно не так много. Пьер Ферма родился на юге Франции в небольшом городке Бомон-де-Ломань, где его отец — Доминик Ферма — был «вторым консулом», т. е. чем-то вроде помощника мэра. Метрическая запись о его крещении от 20 августа 1601 года гласит: «Пьер, сын Доминика Ферма, буржуа и второго консула города Бомона». Мать Пьера, Клер де-Лонг, происходила из семьи юристов.

Доминик Ферма дал своему сыну очень солидное образование. В колледже родного города Пьер приобрел хорошее знание языков: латинского, греческого, испанского, итальянского. Впоследствии он писал стихи на латинском, французском и испанском языках «с таким изяществом, как если бы он жил во времена Августа и провел большую часть своей жизни при дворе Франции или Мадрида».

Ферма славился как тонкий знаток античности, к нему обращались за консультацией по поводу трудных мест при изданиях греческих классиков. Из древних писателей он комментировал Атенея, Полюнуса, СинезуGa, Теона Смирнского и Фронтина, исправил текст Секста Эмпирика. По общему мнению, он мог бы составить себе имя в области греческой филологии.

Но Ферма направил всю силу своего гения на математические исследования. И все же математика не стала его профессией. Ученые его времени не имели возможности посвятить себя целиком любимой науке.

Ферма избирает юриспруденцию. Степень бакалавра была ему присуждена в Орлеане. С 1630 года Ферма переселяется в Тулузу, где получает место советника в Парламенте (т. е. суде). О его юридической деятельности говорится в «похвальном слове», что он выполнял ее «с большой добросовестностью и таким умением, что он славился как один из лучших
юристов своего времени».

В 1631 году Ферма женился на своей дальней родственнице с материнской стороны — Луизе де-Лонг. У Пьера и Луизы было пятеро детей, из которых старший, Самюэль, стал поэтом и ученым. Ему мы обязаны первым собранием сочинений Пьера Ферма, вышедшим в 1679 году. К сожалению, Самюэль Ферма не оставил никаких воспоминаний об отце.

При жизни Ферма о его математических работах стало известно главным образом через посредство обширной переписки, которую он вел с другими учеными. Собрание сочинений, которое он неоднократно пытался написать, так и не было им создано. Да это и неудивительно при той напряженной работе в суде, которую ему пришлось выполнять. Ни одно из его сочинений не было опубликовано при жизни. Однако нескольким трактатам он придал вполне законченный вид, и они стали известны в рукописи
большинству современных ему ученых. Кроме этих трактатов осталась еще обширная и чрезвычайно интересная его переписка. В XVII веке, когда еще не было специальных научных журналов, переписка между учеными играла особую роль. В ней ставились задачи, сообщалось о методах их решения, обсуждались острые научные вопросы.

Корреспондентами Ферма были крупнейшие ученые его времени Декарт, Этьен и Влез Паскали, де-Бееси, Гюйгенс, Торричелли Валлис. Письма посылались либо непосредственно корреспонденту, либо в Париж аббату Мерсенну (соученику Декарта по колледжу); последний размножал их и посылал тем математикам, которые занимались аналогичными вопросами. Но письма ведь почти никогда не бывают только короткими математическими мемуарами. В них проскальзывают живые чувства авторов, которые помогают воссоздать их образы, узнать об их характере и темпераменте. Обычно письма Ферма были проникнуты дружелюбием.

Одной из первых математических работ Ферма было восстановление двух утерянных книг Аполлония «О плоских местах».

Крупную заслугу Ферма перед наукой видят, обыкновенно, во введении им бесконечно малой величины в аналитическую геометрию, подобно тому, как это, несколько ранее, было сделано Кеплером в отношении геометрии древних. Он совершил этот важный шаг в своих относящихся к 1629 году работах о наибольших и наименьших величинах, — работах, открывших собою тот ряд исследований Ферма, который является одним из самых крупных звеньев в истории развития не только высшего анализа вообще, но и анализа бесконечно малых в частности.

В конце двадцатых годов Ферма открыл методы нахождения экстремумов и касательных, которые, с современной точки зрения, сводятся к отысканию производной. В 1636 году законченное изложение метода было передано Мерсенну и с ним могли познакомиться все желающие.

В 1637—1638 годах по поводу «Метода отыскания максимумов и минимумов» у Ферма возникла бурная полемика с Декартом. Последний не понял метода и подверг его резкой и несправедливой критике. В одном из писем Декарт утверждал даже, что метод Ферма «содержит в себе паралогизм». В июне 1638 года Ферма послал Мерсенну для пересылки Декарту новое, более подробное изложение своего метода. Письмо его сдержанно,
но не без внутренней иронии. Он пишет: «Таким образом, обнаруживается, что либо я плохо объяснил, либо г. Декарт плохо понял мое латинское сочинение. Я все же пошлю ему то, что уже написал, и он, несомненно, найдет там вещи, которые помогут ему отказаться от мнения, будто я нашел этот метод случайно и его подлинные основания мне неизвестны».

Ферма ни разу не изменяет своему спокойному тону. Он чувствует свое глубокое превосходство как математика, поэтому не входит в мелочную полемику, а терпеливо старается растолковать свой метод, как это сделал бы учитель ученику.

До Ферма систематические методы вычисления площадей разработал итальянский ученый Кавальєри. Но уже в 1642 году Ферма открыл метод вычисления площадей, ограниченных любыми «параболами» и любыми «гиперболами». Им было показано, что площадь неограниченной фигуры может быть конечной.

Ферма одним из первых занялся задачей спрямления кривых, т. е. вычислением длины их дуг. Он сумел свести эту задачу к вычислению некоторых площадей.

Таким образом, понятие «площади» у Ферма приобретало уже весьма абстрактный характер. К определению площадей сводились задачи на спрямление кривых, вычисление сложных площадей он сводил с помощью подстановок к вычислению более простых площадей. Оставался только шаг, чтобы перейти от площади к еще более абстрактному понятию «интеграл».

Дальнейший успех методов определения «площадей», с одной стороны, и «методов касательных и экстремумов» — с другой, состоял в установлении взаимной связи этих методов. Есть указания на то, что Ферма уже видел эту связь, знал, что «задачи на площади» и «задачи на касательные» являются взаимно обратными. Но он нигде не развил свое открытие сколько-нибудь подробно. Поэтому честь его по праву приписывается
Барроу, Ньютону и Лейбницу, которым это открытие и позволило создать
Дифференциальное и интегральное исчисления.

Несмотря на отсутствие доказательств (из них дошло только одно), трудно переоценить значение творчества Ферма в области теории чисел. Ему одному удалось выделить из хаоса задач и частных вопросов, сразу же возникающих перед исследователем при изучении свойств целых чисел, основные проблемы, которые стали центральными для всей классической теории чисел. Ему же принадлежит открытие мощного общего метода для доказательства теоретико-числовых предложений — так называемого метода неопределенного или бесконечного спуска, о котором будет сказано ниже. Поэтому Ферма по праву может считаться основоположником теории чисел.

В письме к де-Бесси от 18 октября 1640 года Ферма высказал следующее утверждение: если число а не делится на простое число р, то существует такой показатель к, что а—7 делится на р, причем к является делителем р—1. Это утверждение получило название малой теоремы Ферма.

Оно является основным во всей элементарной теории чисел. Эйлер дал этой теореме несколько различных доказательств.

В задаче второй книги своей «Арифметики» Диофант поставил задачу представить данный квадрат в виде суммы двух рациональных квадратов. На полях, против этой задачи, Ферма написал:

«Наоборот, невозможно разложить ни куб на два куба, ни биквадрат на два биквадрата и вообще ни в какую степень, большую квадрата, на две степени с тем же показателем. Я открыл этому поистине чудесное доказательство, но эти поля для него слишком узки». Это и есть знаменитая Великая теорема.

Теорема эта имела удивительную судьбу. В прошлом веке ее исследования привели к построению наиболее тонких и прекрасных теорий, относящихся к арифметике алгебраических чисел. Без преувеличения можно сказать, что она сыграла в развитии теории чисел не меньшую роль, чем задача решения уравнений в радикалах. С той только разницей, что последняя уже решена Галуа, а Великая теорема до сих пор побуждает
математиков к исследованиям.

С другой стороны, простота формулировки этой теоремы и загадочные слова о «чудесном доказательстве» ее привели к широкой популярности теоремы среди не математиков и к образованию целой корпорации «ферматистов», у которых, по словам Дэвенпорта, «смелость значительно превосходит их математические способности». Поэтому Великая теорема стоит на первом месте по числу данных ей неверных доказательств.

Сам Ферма оставил доказательство Великой теоремы для четвертых степеней. Здесь он применил «метод неопределенного или бесконечного спуска», который он описывал в своем письме к Каркави (август 1659 года) следующим образом:

«Если бы существовал некоторый прямоугольный треугольник в целых числах, который имел бы площадь, равную квадрату, то существовал бы другой треугольник, меньший этого, который обладал бы тем же свойством. Если бы существовал второй, меньший первого, который имел бы то же свойство, то существовал бы в силу подобного рассуждения третий, меньший второго, который имел бы то же свойство, и, наконец, четвертый, пятый, спускаясь до бесконечности. Но если задано число, то не
существует бесконечности по спуску меньших его (я все время подразумеваю целые числа). Откуда заключают, что не существует никакого прямоугольного треугольника с квадратной площадью». Именно этим методом были доказаны многие предложения теории чисел, и, в частности, с его помощью Эйлер доказал Великую теорему для п=4 (способом, несколько отличным от способа Ферма), а спустя 20 лет и для п=3.

В прошлом веке Куммер, занимаясь Великой теоремой Ферма, построил арифметику для целых алгебраических чисел определенного вида. Это позволило ему доказать Великую теорему для некоторого класса простых показателей п. В настоящее время справедливость Великой теоремы проверена для всех показателей п меньше 5500.

Отметим также, что Великая теорема связана не только с алгебраической теорией чисел, но и с алгебраической геометрией, которая сейчас интенсивно развивается.

У Ферма есть много других достижений. Он первым пришел к идее координат и создал аналитическую геометрию. Он занимался также задачами теории вероятностей. Но Ферма не ограничивался одной только математикой, он занимался и физикой, где ему принадлежит открытие закона распространения света в средах. Ферма исходил из предположения, что свет пробегает путь от какой-либо точки в одной среде до некоторой точки в другой среде в наикратчайшее время. Применив свой метод максимумов и минимумов, он нашел путь света и установил, в частности, закон преломления света. При этом Ферма высказал следующий общий принцип: «Природа всегда действует наиболее короткими путями», который может считать предвосхищением принципа наименьшего действия Мопертюи — Эйлера.

Одно из последних писем ученого к Каркави получило название «завещание Ферма». Вот его заключительные строки:

«Быть может, потомство будет признательно мне за то, что я показал ему, что древние не все знали, и это может проникнуть в сознание тех, которые придут после меня для передачи факела сыновьям, как говорит великий канцлер Англии, следуя чувствам которого, я добавлю: «Многие будут приходить и уходить, а наука обогащается».

Пьер Ферма скончался 12 января 1665 года во время одной из деловых поездок.

📸 Видео

Великая Теорема Ферма доказана в 1 строкуСкачать

Великая теорема Ферма для n=3 (первая лекция)Скачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

Принципы шифрования, Малая теорема ФермаСкачать

Матан. Теорема Ролля - bezbotvyСкачать

Великая теорема Ферма: истоки, история доказательства и значение для человечестваСкачать