Фалес теорема фалеса ударение

Видео:Теорема Фалеса. 8 класс.Скачать

Словари

Фале́с (около 625 — около 547 до н. э.), древнегреческий мыслитель, родоначальник античной философии и науки, основатель милетской школы. Возводил всё многообразие явлений и вещей к единой первостихии — воде.

ФАЛЕС — ФАЛЕ́С (Thales) (ок. 640 — ок. 546), древнегреческий философ и ученый, основатель так называемой ионийской (см. ИОНИЙСКИЕ ФИЛОСОФЫ) (милетской) школы, родоначальник античной философии и науки; в древности почитался как один из «Семи мудрецов». Аристотель (см. АРИСТОТЕЛЬ) начинает с Фалеса историю метафизики, Евдем (см. ЕВДЕМ из Родоса) — историю астрономии и геометрии.

Происходил из города Милета в Малой Азии, принадлежа к аристократическому роду. Был близок милетскому тирану Фрасибулу (см. ФРАСИБУЛ) и связан с храмом Аполлона Дидимского, покровителя морской колонизации. По свидетельству Диогена Лаэртского (см. ДИОГЕН Лаэртий), бывал в Египте и жил у жрецов, изучая астрономию и геометрию. Видимо, Фалес использовал достижения древневосточной науки египтян, вавилонян и финикийцев. Диоген Лаэртский сообщает, что Фалес установил продолжительность года и разделил его на 365 дней. По словам Геродота, в 585 до н. э. мудрец предсказал полное солнечное затмение.

Имя Фалеса уже в 5 в. до н. э. стало нарицательным для мудреца. Мудрость его истолковывалась по-разному: то как практическая смекалка и изобретательность, то как созерцательная отрешенность (Платон (см. ПЛАТОН (философ))). Предание рисует Фалеса купцом и предпринимателем, гидроинженером, тонким дипломатом и мудрым политиком, провидцем, предсказывающим погоду и затмения.

Из приписываемых Фалесу сочинений ни одно до нас не дошло. Содержание их известно только в передаче более поздних авторов. Аристотель приводит 4 тезиса, которые могут восходить к устному учению Фалеса: 1) все произошло из воды; 2) земля плавает по воде подобно дереву; 3) все полно богов или душа размешана во вселенной; 4) магнит имеет душу, так как движет железо. Таким образом, Фалес впервые сформулировал две основные проблемы греческой натурфилософии (см. НАТУРФИЛОСОФИЯ): проблемы начала и всеобщего. Все многообразие явлений и вещей он сводил к единой основе-первоначалу, которым Фалес считал воду. Отличая душу от тела, душевную жизнь от процессов природы, Фалес, вслед за Гомером (см. ГОМЕР), представлял душу в виде тонкого эфирного вещества. Он считал, что душа, как активная сила и вместе с тем носитель разумности и справедливости, причастна к божественному (разумному и прекрасному) строю вещей.

По свидетельству Прокла (см. ПРОКЛ (философ)), Фалес первый стал доказывать геометрические теоремы; ему принадлежат доказательства следующих положений: 1) круг делится диаметром пополам; 2) в равнобедренном треугольнике углы при основании равны; 3) при пересечении двух прямых образуемые ими вертикальные углы равны; 4) два треугольника равны, если два угла и сторона одного из них равны двум углам и соответствующей стороне другого.

ФАЛЕС (ок. 625 — ок. 547 до н. э.) — древнегреческий мыслитель, родоначальник античной философии и науки, основатель милетской школы. Возводил все многообразие явлений и вещей к единой первостихии — воде.

ФАЛЕС (ок. 640-546 до н.э.), древнегреческий философ, основатель милетской школы. Уроженец Милета в Малой Азии. Фалеса считают отцом греческой философии и причисляют к Семи мудрецам. Сообщается, что Фалес предсказал затмение Солнца (произошедшее, согласно современным вычислениям, 28 мая 585 до н.э.). Он был также умелым политиком и пытался сплотить города Ионии в оборонительный союз против Персии. Будучи военным инженером на службе у царя Лидии Креза, Фалес, как сообщают, пустил реку Галис по новому руслу, а свои деловые качества доказал, захватив монополию на торговлю оливковым маслом. Традиция утверждает, что Фалес познакомил греков с геометрией, которую изучил в Египте. Сочинения Фалеса не сохранились (возможно, он ничего не писал), и то, что мы знаем о его учении, происходит из вторичных источников, в первую очередь из трудов Аристотеля (Метафизика I 3). Фалес считал воду первопринципом, из которого возникают все вещи и в который они распадаются. Согласно Аристотелю, это утверждение основывалось на том наблюдении, что многие предметы, необходимые для жизни (пища, тепло, семена и т.д.), так или иначе содержат влагу. Аристотель приписывает Фалесу изречения: «все полно богов» и «камень (т.е. магнит) имеет душу и потому двигает железо». Присущий философии Фалеса анимизм (иногда его называют гилозоизмом), т.е. вера в то, что материя пронизана жизнью и наделена душой, характерен для представителей ранней ионийской школы.

Фрагменты ранних греческих философов, ч. 1. М., 1989

ФАЛЕС (640 — около 562 или 550 до нашей эры, древнегреческий мыслитель, один из родоначальников античной философии и науки, основатель милетской школы. Фалес — первый из «семи мудрецов». В своем учении полагал, что все произошло из воды; «все полно богов», или «душа-псюхе размешана во Вселенной». Письменных сочинений Фалес не оставил.

Фалес (Thales) Милетский (ок. 624 — ок. 546 до н.э.)

Греческий философ и математик из Милета (Малая Азия). Представитель ионической натурфилософии и основатель милетской школы, с которой начинается история европейской научной космогонии и космологии, физики, географии, метеорологии, астрономии, биологии. Таким образом Фалес считается родоначальником античой и, как следствие, европейской философии и науки. Считался первым из Семи мудрецов Греции. По преданию, путешествовал по странам Востока, учился у египетских жрецов и вавилонских халдеев. В Египте занимался изучением причин наводнений, нашел способ измерения высоты пирамид. По словам Геродота, Фалес предсказал солнечное затмение, наблюдавшееся 28 мая 585 до н.э. Для Фалеса характерен гилозоизм («мир одушевлен и полон богов»). Пытаясь определить основу материального мира, пришел к выводу о том, что ею является вода.

Блаженство тела состоит в здоровье, блаженство ума — в знании.

Что легко? — Давать советы другим.

Соблюдай меру. (начертано у входа в храм Аполлона в Дельфах)

Мудрее всего — время, ибо оно раскрывает все.

О друзьях должно помнить не только в их присутствии, но и в их отсутствии.

Видео:Геометрия 8 класс (Урок№5 - Теорема Фалеса)Скачать

Теорема Фалеса интересные факты. Интересные факты из жизни Фалеса

Видео:Геометрия 8. Урок 8 - Теорема Фалеса - теорияСкачать

Популярные материалы

Today’s:

Видео:Геометрия 8 класс : Теорема ФалесаСкачать

Теорема Фалеса интересные факты. Интересные факты из жизни Фалеса

Интересные факты из жизни Фалеса. По легенде теорема была сформулирована в не сохранившейся «Морской астрономии» Фалеса или Фоки Самосского. Ни одно из античных свидетельств, касающихся Фалеса, с этой теоремой никак напрямую не связано. Возможно, что теорема приписана Фалесу опосредованно, поскольку известно, что он умел измерять высоту обелиска и расстояние до корабля в море; при этих измерениях можно использовать подобие треугольников, а утверждение о пропорциональности сторон подобных треугольников доказывается на основе «теоремы Фалеса». Теорема Фалеса до сих пор используется в морской навигации в качестве правила о том, что столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется курс судов друг на друга. Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла. Основы геометрии Фалес постигал в Египте.

Слайд 4 из презентации «Математические открытия» к урокам математики на тему «История математики»

Размеры: 960 х 720 пикселей, формат: jpg. Чтобы бесплатно скачать слайд для использования на уроке математики, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как…». Скачать всю презентацию «Математические открытия.pptx» можно в zip-архиве размером 622 КБ.

История математики

краткое содержание других презентаций об истории математики

«Математические открытия» — О теореме Пифагора. Теорема Пифагора. Великие открытия Архимеда. Открытия Архимеда. Фалес Милетский. Пифагорейцы. Творцы математики и их открытия. Сочинения Пифагора. Интересные факты из жизни Фалеса. Эратосфен Киренский. Труды Эратосфена. Мудрец. Решето Эратосфена. Теорема Фалеса. Начала Евклида. Описание монохорда.

«Математика в Греции» — Греческая математика поражает прежде всего красотой и богатством содержания. Успехи пифагорейцев в стереометрии были значительными. Математика в Древней Греции. Теэтет и Евклид установили классификацию квадратичных иррациональностей. Глава II. 1.2 Поворотный пункт в истории античной математики. Пифагорейцы заложили основы геометрической алгебры.

«Математика в США» — Джон фон Нейман. Чёрч стал профессором математики в Принстоне в 1929 году. Такой ответ поставил часового в тупик. Владимир Александрович Воеводский — российский и американский математик, преподаватель. Обозначение нуля также применялось для обозначения бесконечности. Американские премии в области математики.

«История математики в России» — Способ умножения с «помощью рук». Сухарева башня. Курбатов. Согласно показанию Курбатова, желающих учиться в школе было много. Материальная сторона дела была передана в Оружейную палату. Труд Магницкого. Первая математическая школа в Москве. Образование. А. Курбатов предложил Петру I математика. Арифметика.

«История появления математики» — Кипу, использовались инками для записи чисел. Рене Декарт. Листья на ветке растения. Математика в разное время. М.В.Остроградский. Интересные факты. Цифры майя. Математика. Математический закон Бенфорда. Великие математики. Исаак Ньютон. Разделы математики. История математики. Как появилась математика.

Видео:ТЕОРЕМА ФАЛЕСА доказательство 384 Атанасян 8 классСкачать

Теорема Фалеса ударение. Замечания

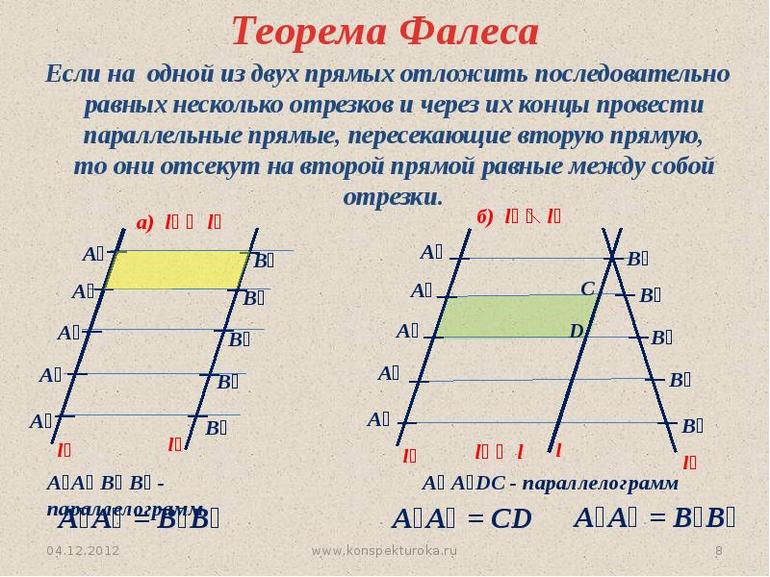
• В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также не важно, где находятся отрезки на секущих.

• Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.

Доказательство в случае секущих

Рассмотрим вариант с несвязанными парами отрезков: пусть угол пересекают прямые A A 1 | | B B 1 | | C C 1 | | D D 1 <displaystyle AA_||BB_||CC_||DD_> и при этом A B = C D .

1. Проведём через точки A и C прямые, параллельные другой стороне угла. A B 2 B 1 A 1 <displaystyle AB_B_A_> и C D 2 D 1 C 1 <displaystyle CD_D_C_> . Согласно свойству параллелограмма: A B 2 = A 1 B 1 <displaystyle AB_=A_B_> и C D 2 = C 1 D 1 <displaystyle CD_=C_D_> .

Видео:Теорема Фалеса. Практическая часть - решение задачи. 8 класс.Скачать

Как разделить отрезок на 3 равные части по теореме Фалеса. Теорема Фалеса и деление отрезка в заданном отношении

Давно о геометрии не говорили, а о теореме ФАлеса (или ФалЕса?) вообще мало говорят. Хотя она весьма полезна. Начнем с формулировки, которая весьма не вразумительна, чем и объясняется не популярность данной теоремы.

Мутно, долго, не понятно. Мне больше нравится другая формулировка.

Тоже не понятно, но элегантно и коротко.

Задачи, которые решаются с помощью данной теоремы, довольно специфичны. Но есть одна задача на построение, которую можно встретить в реальной жизни. Это задача о делении отрезка в заданном отношении.

Суть вопроса: Дан отрезок. Его нужно поделить на два куска, чтобы их длины относились, как 2 : 5. Кусков может быть сколько угодно и отношение, может быть каким угодно. Алгебраически задача решается крайне легко: находим общее количество частей (2 + 5 = 7), делим длину отрезка на общее количество частей, находим длину каждого куска.

Но алгебраическое решение не всегда прокатывает. Например, мы не можем найти длину отрезка, или при делении получаются не целые числа. Тогда можно воспользоваться геометрическим способом.

Во-первых, проводим луч из конца отрезка. Любой, в любую сторону.

Дальше, на этом луче от точки А откладываем 7 (общее количество частей) равных отрезков.

Последнюю получившуюся точку — J соединяем с точкой В, а затем через каждую точку луча проводим прямую параллельную JB.

Таким образом, мы разделили отрезок АВ на 7 равных частей (по теореме Фалеса). Отсчитываем две части и ставим точку. Получаем: AK : KB = 2 : 5.

Вот таким простым образом, вы можете поделить свою комнату с соседом в любом отношении. Если вам кажется, что построение такого количества параллельных прямых дело сложное, то подумайте о перпендикулярах.

Видео:МЕРЗЛЯК-8 ГЕОМЕТРИЯ. ТЕОРЕМА ФАЛЕСА. ПАРАГРАФ-11. ТЕОРИЯСкачать

Докажите теорему Фалеса. Обобщенная теорема Фалеса

Определение, которое мы сформулировали, является избыточным – чтобы треугольники были подобны, не нужно требовать и пропорциональности трех пар сторон, и равенства трех углов.

Для того чтобы убедиться в том, что два треугольника являются подобными, существуют признаки подобия треугольников (по аналогии с признаками равенства). И в них не требуется проверять все утверждения, перечисленные в определении.

Чтобы разобраться в этом, рассмотрим очень древний и очень удобный геометрический инструмент – теорему Фалеса. Фалес Милетский, именем которого названа теорема, жил более 2,5 тысяч лет назад.

Рис. 8. Фалес Милетский

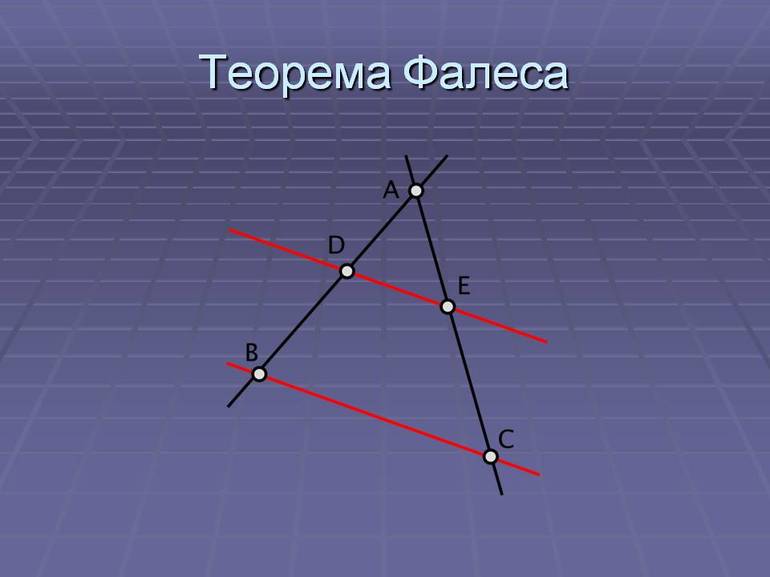
Теорема Фалеса достаточно наглядна и не вызывает особых сомнений даже без строгого доказательства: если параллельные прямые отсекают равные отрезки на одной стороне угла, то они отсекают равные отрезки и на другой стороне (см. рис. 9).

Рис. 9. Иллюстрация к теореме Фалеса

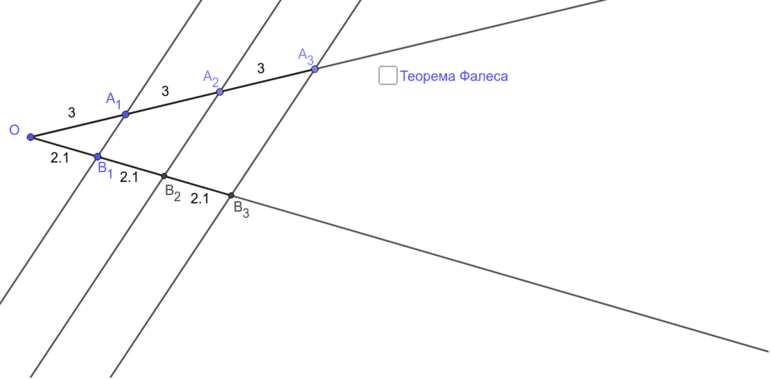
Более общая формулировка этой теоремы (ее еще называют обобщенной теоремой Фалеса или теоремой о пропорциональных отрезках ): параллельные прямые отсекают на сторонах угла пропорциональные отрезки .

Т. е. если пересечь угол несколькими параллельными прямыми (в отличие от классической формулировки можно начертить прямые на разных расстояниях друг от друга), то отношение двух отрезков на одной стороне угла будет равно отношению соответствующих отрезков на второй стороне (см. рис. 10):

Рис. 10. Иллюстрация к теореме Фалеса

Доказывать эти теоремы мы пока не умеем. Но обязательно сделаем это чуть позже. Пока возьмем их на вооружение как известные нам факты.

Теорема Фалеса в жизни

Чтобы проиллюстрировать применение теоремы Фалеса, рассмотрим такой пример.

Пусть два корабля движутся так, что их курс друг относительно друга не меняется (под курсом в данном случае мы понимаем угол между направлением движения судна и направлением на второе судно) (см. рис. 11).

Рис. 11. Курс двух движущихся кораблей друг относительно друга не меняется

Тогда ясно, что при неизменности ситуации, неизбежно столкновение (поскольку из равенства углов следует, что прямые, соединяющие корабли, параллельны друг другу, а значит, за равные промежутки времени они проходят одинаковые расстояния и должны сойтись в одной точке – вершине угла) (см. рис. 12).

Рис. 12. За равные промежутки времени корабли проходят одинаковые расстояния и должны сойтись в одной точке

Это можно использовать для предотвращения аварий в море. Ведь чем раньше капитаны кораблей узнают о вероятности столкновения, тем больше шансов его избежать.

В отличие от автомобилей большие грузовые суда имеют очень большой тормозной путь (т. к. сила сопротивления со стороны воды очень маленькая, а инертность из-за большой массы огромная). Так, у нефтяных танкеров тормозной путь может быть длиной несколько десятков километров.

Видео:ТЕОРЕМА ФАЛЕСА . §11 геометрия 8 классСкачать

Теорема Фалеса — формулировка, доказательство и применение

Видео:Теорема ФалесаСкачать

Краткое описание

Фалес хорошо известен в истории как талантливый геометр. Именно этому человеку многие учёные приписывают открытие и доказательство многих теорем. Фалес смог разработать весьма интересный способ определения точного расстояния от берега до видимого невооружённым взглядом водного транспорта. Некоторые историки склонны полагать, что именно для этих целей учёный использовал признак некоего сходства прямоугольных треугольников. Современные последователи великого математика высоко ценят все его достижения, что он смог вывести и доказать многочисленные теоремы, законы.

Наиболее логическое доказательство правильности предположений на основании единых положений, принятых за проверенные истины, было изобретено именно греками. Сегодня историкам трудно сказать, что именно в научном перечне принадлежит Фалесу. Конечно, благодаря этому талантливому человеку Греция обрела не только философа и математика, но и естествоиспытателя.

Перед изучением теоремы обязательно нужно понять, что параллелограмм — это самый обычный четырёхугольник, у которого все противоположные стороны попарно параллельны. А вот трапеция является специфическим четырёхугольником, у которого две стороны параллельны друг другу, а две другие стороны обладают противоположными характеристиками. Изучение этой темы состоит из нескольких частей, так как первым делом нужно ознакомиться с теорией, а только потом можно приступать к решению задач.

Видео:Фалес и его открытияСкачать

Основные понятия

Фалесом было доказано, что две прямые линии RF и NS называются параллельными исключительно в том случае, если они проложены в одной плоскости и не пересекаются между собой вне зависимости от длины. Это правило всегда обозначают как RF || NS.

Абсолютно все существующие точки конкретной прямой располагаются на неизменном расстоянии от второй линии. А это значит, что все линии, которые параллельны одной прямой, являются параллельными между собой. Математики полагают, что итоговый угол между параллельными линиями приравнивается 0. Но это утверждение актуально только в том случае, если у отрезков одинаковые направления и они расположены под углом 180 градусов.

В качестве наглядного примера можно рассмотреть ситуацию, когда перпендикуляры RF, NS, EF относятся к одной и той же прямой РЕ и параллельны между собой. При этом прямая РЕ перпендикулярна ко всем остальным линиям. Итоговая длина сформированного отрезка перпендикуляра, расположенного между двумя параллельными прямыми, соответствует расстоянию средних линий. При изучении пространственной теоремы обязательно нужно понимать, что сразу восемь углов возникает при пересечении двух параллельных прямых третьей прямойю

Представленная специалистами формулировка теоремы Фалеса содержит много нюансов, в которых обязательно должен разбираться каждый человек, планирующий решать различные математические задачи. В противном случае будет сложно избежать самых распространённых ошибок. Даже кратко изложенная теория позволяет разобраться в главных математических тонкостях. Чтобы ученику стало понятно то, как именно нужно использовать теорему, можно задействовать специальные таблицы, которые помогут расширить итоговые математические возможности.

Видео:Бомбическая задача на теорему ФалесаСкачать

Научное пояснение значений

Если постараться поочерёдно отложить сразу несколько одинаковых отрезков только на одной из двух прямых линий, а потом провести прямые через конечные точки, которые смогут пересечь вторую прямую, то именно на второй прямой они смогут отсечь равные отрезки. Развёрнутая формулировка этой темы в геометрии носит название теоремы о пропорциональных геометрических отрезках. В качестве наглядного примера следует ознакомиться с этой формулой: S1S2/N1В2 = S2S3/N2N3 = S1S3/N1N3.

Важные нюансы:

• Востребованная теорема греческого математика является частным случаем закона о пропорциональных отрезках, так как идентичные отрезки можно считать пропорциональными с элементарным коэффициентом ровности, который равняется единице.
• В изучаемой теореме нет каких-либо ограничений и требований на взаимное расположение всех секущих. Это связано с тем, что она верна как для пересекающихся прямых, так и для параллельных линий. На итоговый результат совершенно не влияет то, где находятся отрезки на секущих.

Для изучения всех нюансов этой темы необходимо рассмотреть вариант, который демонстрирует ситуацию с несвязанными парами отрезков. К примеру: существующий угол пересекает прямые LL1 || ВВ1 || СС1 || КК1 и при этом LB = СК. Через точки L и С проводят прямую линию, которая будет расположена параллельно другой стороне сформированного угла LB2В1L1 и СК2К1С1. Свойства параллелограмма тоже имеют свои особенности:

Треугольники ? JSS2 и ? СКК2 равны. Они построены на основании второго признака равенства геометрических фигур. Если целью задачи является безусловное доказательство при параллельных прямых, тогда нужно выполнить несколько несложных действий. Следует провести прямую SC. Углы SCK и JSC равны как внутренние накрест лежащие при прямых СК и JS, а также секущей SC. А вот углы JCS и CSK равны как внутренние накрест проложенные линии при параллельных прямых JC и SK, секущий SC. Тогда по второму признаку равенства треугольников геометрические фигуры JSC и KCS равны. Из этого вытекает, что JC = SK и JS = СК.

Видео:Геометрия 8. Урок 9 - Теорема Фалеса - задачиСкачать

Ключевые особенности теоремы

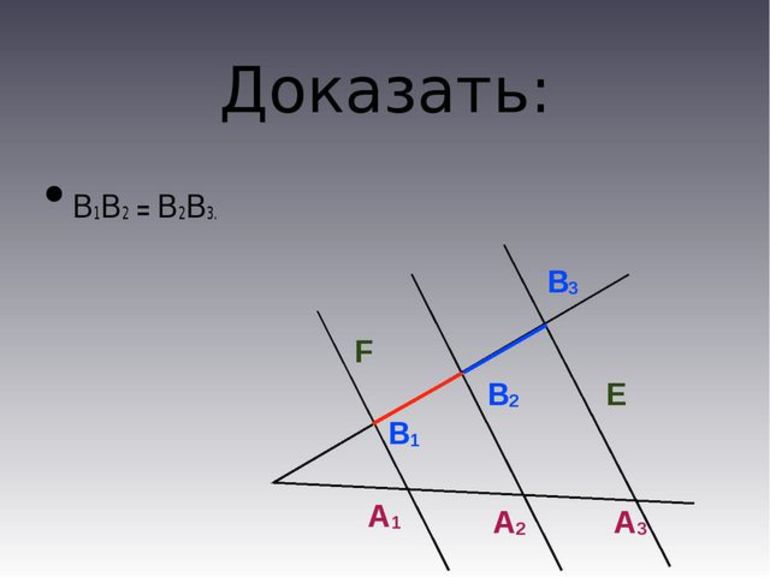
Когда учащийся попробует на одной из двух прямых линий отложить разные отрезки, а потом через их концы провести параллельные линии, которые будут пересекать вторую прямую, то в итоге на второй прямой они обязательно отсекут идентичные между собой отрезки. Даже в школьной математике часто пользуются обобщённой теоремой Фалеса: те отрезки, которые формируются только благодаря параллельным прямым на одной линии, являются пропорциональными по отношению к другой прямой линии.

Записи с идеями Фалеса не удалось сохранить до наших дней, из-за чего историкам приходится восстанавливать информацию из разных источников. Специалистам удалось доказать, что математик из Греции вывел 7 теорем для геометрии. Основное правило гласит, что если параллельные линии, у которых пересекаются стороны угла, отсекают только на одной его стороне равные отрезки, то аналогичная ситуация происходит и на другой его стороне.

Наглядное доказательство

В качестве примера можно взять точки Н1, Н2 и Н3, которые служат для обозначения пересечения используемых параллельных отрезков только с одной стороны угла. А вот для обозначения точек пересечения этих прямых с другой стороны угла используется К1, К2 и К3. Если через точку К2 провести небольшую прямую Т1 и Т2, а также параллельную Н1 и Н2, то в итоге получится обычный параллелограмм: Н1Т1КН2 и Н2К2Т2Н3. Из этого результата можно понять, что Н1Н2 = Т1К2 и Н2Н3 = К2Т2. Этот результат был достигнут благодаря тому, что Н1Н2 = Н2Н3, а Т1К1 = К2Т2.

💥 Видео

Теорема фалеса. Теорема о пропорциональных отрезках - геометрия 8 классСкачать

Теорема ФалесаСкачать

Урок 31. Теорема Фалеса (8 класс)Скачать

Теорема Фалеса. Доказательство.Скачать

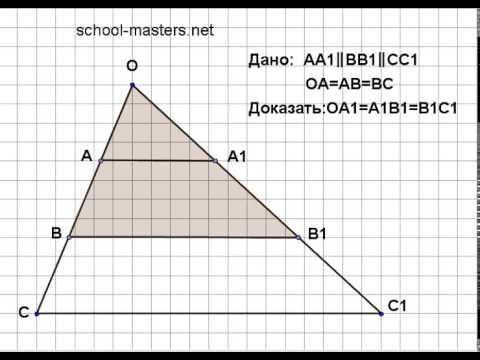
Обобщенная теорема Фалеса. Доказательство.Скачать

Теорема Фалеса. Практическая часть - решение задачи. 8 класс.Скачать

Теорема Фалеса. Примеры решения заданий.Скачать

Теорема Фалеса. Теорема о пропорциональных отрезках. Экстра Математика ЕГЭСкачать